Mathematics, a language of numbers and symbols, often intrigues us with its complex relationships and functions. One such function that frequently pops up in trigonometry is the secant function. Many students and enthusiasts often wonder, "Is secant 1/cos?" This question, while seemingly simple, opens the door to a deeper understanding of trigonometric functions and their relationships. By exploring the secant function, we can unravel the connections it shares with other trigonometric entities, particularly the cosine function.
In the realm of trigonometry, the secant function plays a pivotal role, analogous to its more commonly known counterpart, the cosine function. The question "is secant 1/cos" often serves as a gateway for learners to delve into the intricate web of trigonometric identities. Understanding the secant function not only helps in solving mathematical problems but also enhances our comprehension of the geometrical interpretations inherent in trigonometry. The relationship between secant and cosine is fundamental, and exploring it can provide valuable insights into the broader mathematical landscape.
As we embark on this mathematical exploration, let's dissect the secant function, its properties, and its applications. By examining how secant relates to cosine and other trigonometric functions, we can appreciate the elegant symmetry and functionality of trigonometry. This article aims to provide a comprehensive overview of the secant function, its significance, and its practical use in various mathematical contexts. Join us as we venture into the world of trigonometry and uncover the mysteries behind the secant function.
Read also:Reliable Emergency Alerts Your Lifeline In Urgent Situations
Table of Contents
- What is the Secant Function?
- Secant Function in Trigonometry
- Is Secant 1/Cos?
- Mathematical Proof of Sec = 1/Cos
- Geometrical Interpretation of Secant
- Applications of the Secant Function
- Secant in Calculus and Analysis
- Secant and Other Trigonometric Functions
- Common Misconceptions about Secant
- How Does Secant Relate to Cosine?
- Secant Function in the Real World
- Graphical Representation of Secant
- Historical Context of the Secant Function
- Frequently Asked Questions
- Conclusion
What is the Secant Function?
The secant function, commonly denoted as sec(θ), is one of the six fundamental trigonometric functions. In trigonometry, it is defined as the reciprocal of the cosine function. Mathematically, this can be expressed as sec(θ) = 1/cos(θ). The secant function is particularly important in contexts where calculating the reciprocal of cosine is necessary.
Historically, the secant function was used extensively in navigation and astronomy. Today, it finds applications in various fields such as engineering, physics, and computer graphics. Its significance lies in the fact that it helps in determining ratios of sides in right-angled triangles, especially when dealing with angles that result in undefined values for cosine.
The secant function is defined for all real numbers except where the cosine function is zero. These points correspond to odd multiples of 90 degrees or π/2 radians, where the cosine function equals zero, leading to a division by zero in the secant function. Thus, the domain of the secant function is restricted to exclude these points.
Secant Function in Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. Within this framework, the secant function serves as an extension of the cosine function. When exploring trigonometric identities, the secant function often appears alongside its counterparts: sine, cosine, tangent, cosecant, and cotangent.
One of the fundamental identities involving the secant function is its reciprocal relationship with cosine: sec(θ) = 1/cos(θ). This identity is central to solving many trigonometric problems and simplifying complex expressions. Additionally, the secant function is often used in conjunction with the Pythagorean identity, which relates sine and cosine functions to the unit circle.
In trigonometric equations and identities, the secant function plays a crucial role. For instance, in the identity sec²(θ) = 1 + tan²(θ), the secant function is expressed in terms of the tangent function. Understanding such identities is essential for simplifying expressions and solving equations involving trigonometric functions.
Read also:Comprehensive Guide To Managing Eczema Of Face Naturally
Is Secant 1/Cos?
Yes, the secant function is indeed the reciprocal of the cosine function. This means that sec(θ) can be expressed as 1/cos(θ). This relationship is fundamental to trigonometry, serving as a basis for various calculations and transformations involving trigonometric functions.
Understanding this relationship helps in grasping the broader concept of reciprocal trigonometric functions. Just as secant is the reciprocal of cosine, other functions have their reciprocals: cosecant is the reciprocal of sine, and cotangent is the reciprocal of tangent. These relationships form the backbone of trigonometric identities and equations.
The question "is secant 1/cos" often arises in the context of solving trigonometric equations or simplifying expressions. Recognizing the secant function as the reciprocal of cosine allows mathematicians and students to manipulate and solve equations more effectively, leading to a deeper understanding of trigonometric concepts.
Mathematical Proof of Sec = 1/Cos
To mathematically prove that sec(θ) = 1/cos(θ), we begin by examining the definition of the secant function. By definition, the secant function is the reciprocal of the cosine function. Therefore, if cos(θ) is defined as the ratio of the adjacent side to the hypotenuse in a right-angled triangle, sec(θ) can be expressed as the ratio of the hypotenuse to the adjacent side.
Consider a right-angled triangle with angle θ. Let the adjacent side be "a," the hypotenuse be "h," and the opposite side be "o." According to the definition of cosine, we have cos(θ) = a/h. The reciprocal of this expression gives us sec(θ) = h/a, which is equivalent to 1/cos(θ).
This proof is rooted in the fundamental properties of right-angled triangles and the definitions of trigonometric functions. By understanding these definitions, we can confidently assert the reciprocal relationship between secant and cosine, reinforcing the identity sec(θ) = 1/cos(θ).
Geometrical Interpretation of Secant
From a geometrical perspective, the secant function can be visualized using the unit circle. In the context of the unit circle, the secant of an angle θ is the length of the line segment from the origin to the point where the line perpendicular to the x-axis intersects the extended radius that forms the angle θ.
To better understand this, imagine a unit circle centered at the origin of a coordinate plane. As the angle θ increases from 0 to 90 degrees, the cosine of θ decreases from 1 to 0. Consequently, the secant of θ, being the reciprocal of cosine, increases from 1 to infinity. This geometrical interpretation highlights how the secant function relates to the concept of extending the radius of the unit circle.
By visualizing the secant function in this manner, we can appreciate its relationship with the unit circle and other trigonometric functions. This understanding aids in solving geometric problems and provides a more intuitive grasp of trigonometric concepts.
Applications of the Secant Function
The secant function finds applications across various fields, including engineering, physics, and computer graphics. In engineering, it is often used in the analysis and design of mechanical systems, particularly in contexts involving rotational motion and oscillations.
In physics, the secant function is employed to describe phenomena involving waves and oscillations. It helps in modeling situations where the reciprocal of the cosine function is required, such as in the analysis of light waves and sound waves. Furthermore, the secant function is used in the calculation of angles and distances in optics and acoustics.
In computer graphics, the secant function is utilized in rendering and animation techniques. It aids in calculating lighting angles, reflections, and refractions, contributing to the creation of realistic visual effects in digital media. The versatility of the secant function makes it a valuable tool in various scientific and technological domains.
Secant in Calculus and Analysis
In the realm of calculus and analysis, the secant function plays a significant role in the study of limits, derivatives, and integrals. One of the fundamental applications of the secant function is in the calculation of derivatives of trigonometric functions, particularly when dealing with expressions involving reciprocal functions.
For instance, the derivative of the secant function can be expressed as the product of secant and tangent functions: d/dθ(sec(θ)) = sec(θ)tan(θ). This derivative is essential in solving problems involving rates of change and motion in physics and engineering.
Moreover, the secant function is used in the evaluation of integrals, particularly in the context of trigonometric substitution. By substituting secant and tangent functions into integrals, mathematicians can simplify complex expressions and solve integrals that would otherwise be challenging to evaluate.
Secant and Other Trigonometric Functions
The secant function is closely related to other trigonometric functions, forming a network of identities and relationships that are fundamental to trigonometry. One of the key relationships is the reciprocal nature of the secant and cosine functions: sec(θ) = 1/cos(θ).
Additionally, the secant function can be expressed in terms of the tangent function through the identity sec²(θ) = 1 + tan²(θ). This identity highlights the interconnectedness of trigonometric functions and aids in simplifying expressions and solving equations.
The secant function is also related to the sine and cosecant functions. While the secant function is the reciprocal of cosine, the cosecant function is the reciprocal of sine. Understanding these reciprocal relationships is crucial for solving trigonometric equations and proving identities.
Common Misconceptions about Secant
Despite its importance, the secant function is often misunderstood or misrepresented in mathematical discussions. One common misconception is that the secant function is identical to the tangent function. While both functions are related, they are distinct in their definitions and applications.
Another misconception is that the secant function is undefined for all angles where the cosine function is zero. While it is true that secant is undefined at these points, the misconception arises from the assumption that secant is undefined for all angles, which is incorrect. The secant function is defined for all angles except odd multiples of 90 degrees or π/2 radians.
Clarifying these misconceptions is essential for a proper understanding of the secant function and its role in trigonometry. By addressing these misunderstandings, mathematicians and educators can ensure that students have a clear and accurate comprehension of trigonometric functions.
How Does Secant Relate to Cosine?
The relationship between secant and cosine is a cornerstone of trigonometry. As previously mentioned, the secant function is the reciprocal of the cosine function, meaning sec(θ) = 1/cos(θ). This reciprocal relationship forms the basis for many trigonometric identities and equations.
In addition to their reciprocal nature, secant and cosine share a geometric relationship in the context of the unit circle. As the cosine of an angle decreases, the secant of that angle increases, illustrating the inverse relationship between the two functions.
Understanding how secant relates to cosine is crucial for solving trigonometric problems and proving identities. By recognizing the interplay between these functions, mathematicians can simplify expressions, solve equations, and gain a deeper insight into the properties of trigonometric functions.
Secant Function in the Real World
The secant function, though primarily a mathematical concept, has numerous real-world applications. In engineering, it is used to analyze and design systems involving rotational motion, such as gears, pulleys, and turbines. The secant function helps engineers calculate angles, distances, and forces in these systems.
In physics, the secant function is employed to model wave phenomena, including sound and light waves. It aids in the calculation of angles and distances in optical systems, such as lenses and mirrors, contributing to the design and analysis of optical instruments.
In computer graphics, the secant function plays a role in rendering and animation, helping create realistic lighting effects and reflections in digital media. Its ability to model angles and distances makes it a valuable tool in the creation of visual effects and animations.
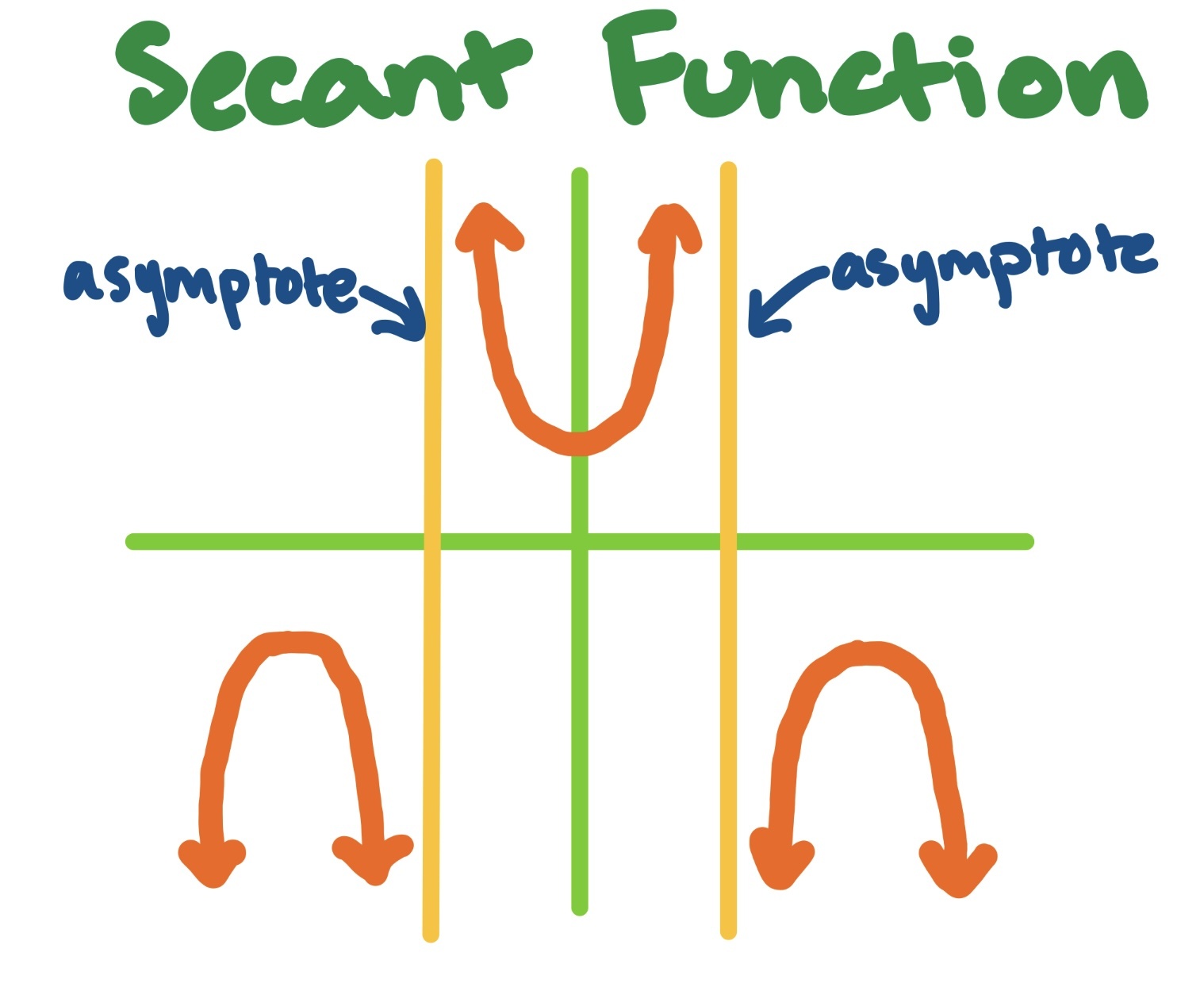
Graphical Representation of Secant
The graphical representation of the secant function provides valuable insights into its properties and behavior. On a graph, the secant function is characterized by its periodic nature, with discontinuities at odd multiples of 90 degrees or π/2 radians, where the cosine function is zero.
The graph of the secant function is related to the graph of the cosine function, as it is the reciprocal of cosine. As the cosine function approaches zero, the secant function approaches infinity, resulting in vertical asymptotes on the graph.
By analyzing the graph of the secant function, mathematicians can gain a better understanding of its properties, such as its domain, range, and period. This understanding is essential for solving trigonometric problems and visualizing the relationships between trigonometric functions.
Historical Context of the Secant Function
The secant function has a rich historical context, with its origins tracing back to ancient civilizations. It was first used by astronomers and mathematicians in the study of celestial bodies and navigation. The term "secant" is derived from the Latin word "secare," meaning "to cut," reflecting its geometric interpretation as a line that cuts through a circle.
In the Middle Ages, the secant function was further developed by Islamic mathematicians, who used it to solve problems in astronomy and geography. The function was later adopted by European mathematicians during the Renaissance, who incorporated it into the study of trigonometry.
Today, the secant function is an integral part of trigonometry, with applications in various fields such as engineering, physics, and computer graphics. Its historical significance underscores its importance as a mathematical tool and its enduring relevance in modern mathematics.
Frequently Asked Questions
- What is the secant function?
The secant function is a trigonometric function defined as the reciprocal of the cosine function. It is denoted as sec(θ) and is expressed as sec(θ) = 1/cos(θ).
- Why is the secant function important?
The secant function is important because it provides a way to calculate the reciprocal of the cosine function, which is useful in solving trigonometric equations and simplifying expressions.
- How is the secant function used in real-world applications?
The secant function is used in engineering, physics, and computer graphics to model angles and distances, analyze rotational motion, and create realistic visual effects.
- Is the secant function defined for all angles?
No, the secant function is undefined for angles where the cosine function is zero, specifically at odd multiples of 90 degrees or π/2 radians.
- What is the relationship between secant and cosine?
The secant function is the reciprocal of the cosine function, meaning sec(θ) = 1/cos(θ). This reciprocal relationship is fundamental to trigonometry.
- What are some common misconceptions about the secant function?
Common misconceptions include the belief that the secant function is identical to the tangent function and that it is undefined for all angles. In reality, the secant function is distinct from tangent and is only undefined at specific points where cosine is zero.
Conclusion
The secant function, with its reciprocal relationship to the cosine function, is a fundamental component of trigonometry. By understanding the secant function's properties, applications, and graphical representation, we gain valuable insights into the broader realm of trigonometric functions and their interconnectedness. The secant function's significance extends beyond mathematics, finding applications in various scientific and technological fields, underscoring its enduring relevance and utility.
Through this exploration of the secant function, we have uncovered the intricacies and nuances that define its role in mathematics. By addressing common misconceptions and highlighting its applications, we can appreciate the secant function's importance and its contribution to our understanding of the mathematical world. As we continue to delve into the complexities of trigonometry, the secant function remains a vital tool, guiding us through the intricacies of angles, ratios, and relationships.
In conclusion, the secant function's relationship to cosine, its historical context, and its real-world applications make it a valuable and indispensable part of mathematical study. By embracing the secant function and its connections, we enrich our mathematical knowledge and enhance our problem-solving capabilities.